@article{chen2020neurodiffeq,
title={NeuroDiffEq: A Python package for solving differential equations with neural networks},
author={Chen, Feiyu and Sondak, David and Protopapas, Pavlos and Mattheakis, Marios and Liu, Shuheng and Agarwal, Devansh and Di Giovanni, Marco},
journal={Journal of Open Source Software},
volume={5},
number={46},
pages={1931},
year={2020}
}
🔥🔥🔥Did you know that neurodiffeq supports solution bundles and can be used to solve reverse problems? See here!
🎓 Already familiar with neurodiffeq? 👇 Jump to FAQs.
neurodiffeq is a package for solving differential equations with neural networks. Differential equations are equations that relate some function with its derivatives. They emerge in various scientific and engineering domains. Traditionally these problems can be solved by numerical methods (e.g. finite difference, finite element). While these methods are effective and adequate, their expressibility is limited by their function representation. It would be interesting if we can compute solutions for differential equations that are continuous and differentiable.
As universal function approximators, artificial neural networks have been shown to have the potential to solve ordinary differential equations (ODEs) and partial differential equations (PDEs) with certain initial/boundary conditions. The aim of neurodiffeq is to implement these existing techniques of using ANN to solve differential equations in a way that allow the software to be flexible enough to work on a wide range of user-defined problems.
Like most standard libraries, neurodiffeq is hosted on PyPI. To install the latest stable relesase,
pip install -U neurodiffeq # '-U' means update to latest versionAlternatively, you can install the library manually to get early access to our new features. This is the recommended way for developers who want to contribute to the library.
git clone https://github.com/NeuroDiffGym/neurodiffeq.git
cd neurodiffeq && pip install -r requirements
pip install . # To make changes to the library, use `pip install -e .`
pytest tests/ # Run tests. Optional.We are happy to help you with any questions. In the meantime, you can checkout the FAQs.
To view complete tutorials and documentation of neurodiffeq, please check Official Documentation.
In addition to the documentations, we have recently made a quick walkthrough Demo Video with slides.
from neurodiffeq import diff
from neurodiffeq.solvers import Solver1D, Solver2D
from neurodiffeq.conditions import IVP, DirichletBVP2D
from neurodiffeq.networks import FCNN, SinActvHere we solve a non-linear system of two ODEs, known as the Lotka–Volterra equations. There are two unknown functions (u and v) and a single independent variable (t).
def ode_system(u, v, t):
return [diff(u,t)-(u-u*v), diff(v,t)-(u*v-v)]
conditions = [IVP(t_0=0.0, u_0=1.5), IVP(t_0=0.0, u_0=1.0)]
nets = [FCNN(actv=SinActv), FCNN(actv=SinActv)]
solver = Solver1D(ode_system, conditions, t_min=0.1, t_max=12.0, nets=nets)
solver.fit(max_epochs=3000)
solution = solver.get_solution()solution is a callable object, you can pass in numpy arrays or torch tensors to it like
u, v = solution(t, to_numpy=True) # t can be np.ndarray or torch.TensorPlotting u and v against their analytical solutions yields something like:
Here we solve a Laplace Equation with Dirichlet boundary conditions on a rectangle. Note that we choose Laplace equation for its simplicity of computing analytical solution. In practice, you can attempt any nonlinear, chaotic PDEs, provided you tune the solver well enough.
Solving a 2-D PDE system is quite similar to solving ODEs, except there are two variables x and y for boundary value problems or x and t for initial boundary value problems, both of which are supported.
def pde_system(u, x, y):
return [diff(u, x, order=2) + diff(u, y, order=2)]
conditions = [
DirichletBVP2D(
x_min=0, x_min_val=lambda y: torch.sin(np.pi*y),
x_max=1, x_max_val=lambda y: 0,
y_min=0, y_min_val=lambda x: 0,
y_max=1, y_max_val=lambda x: 0,
)
]
nets = [FCNN(n_input_units=2, n_output_units=1, hidden_units=(512,))]
solver = Solver2D(pde_system, conditions, xy_min=(0, 0), xy_max=(1, 1), nets=nets)
solver.fit(max_epochs=2000)
solution = solver.get_solution()The signature of solution for a 2D PDE is slightly different from that of an ODE. Again, it takes in either numpy arrays or torch tensors.
u = solution(x, y, to_numpy=True)Evaluating u on [0,1] × [0,1] yields the following plots
| ANN-Based Solution | Residual of PDE |
|---|---|
 |
 |
A monitor is a tool for visualizing PDE/ODE solutions as well as history of loss and custom metrics during training. Jupyter Notebooks users need to run the %matplotlib notebook magic. For Jupyter Lab users, try %matplotlib widget.
from neurodiffeq.monitors import Monitor1D
...
monitor = Monitor1D(t_min=0.0, t_max=12.0, check_every=100)
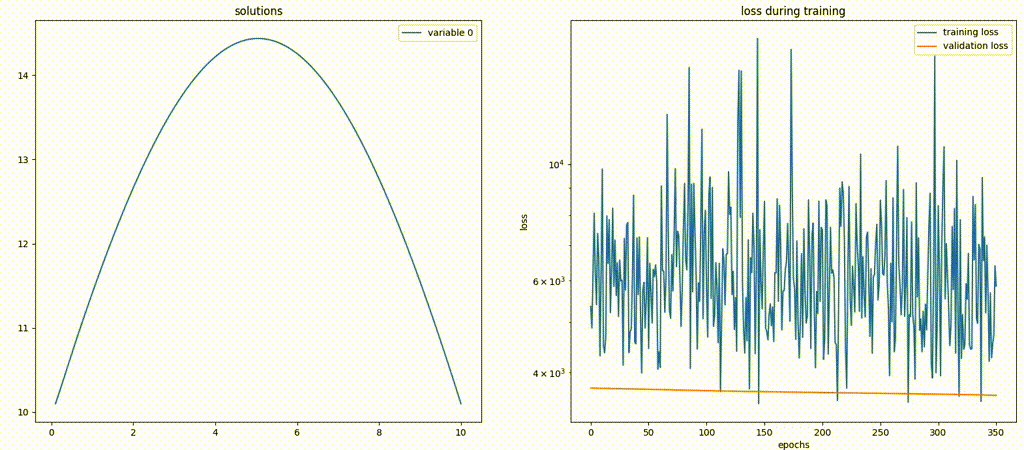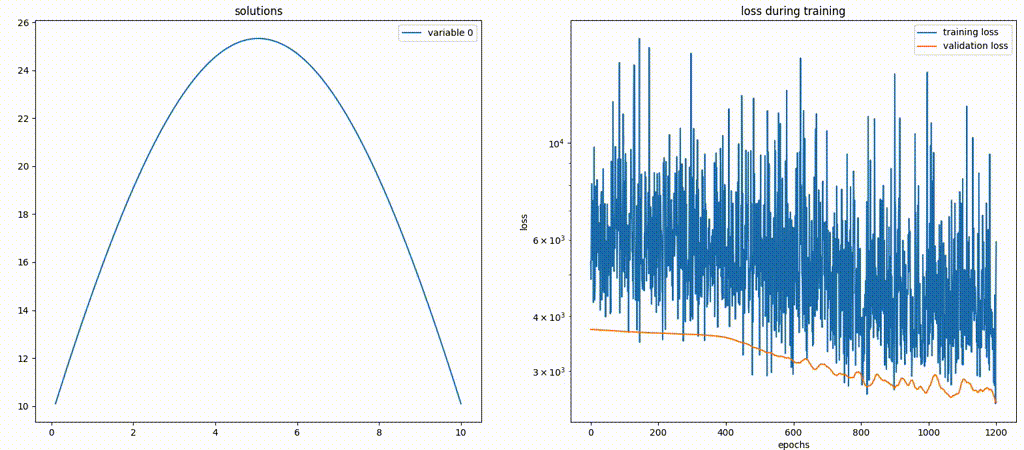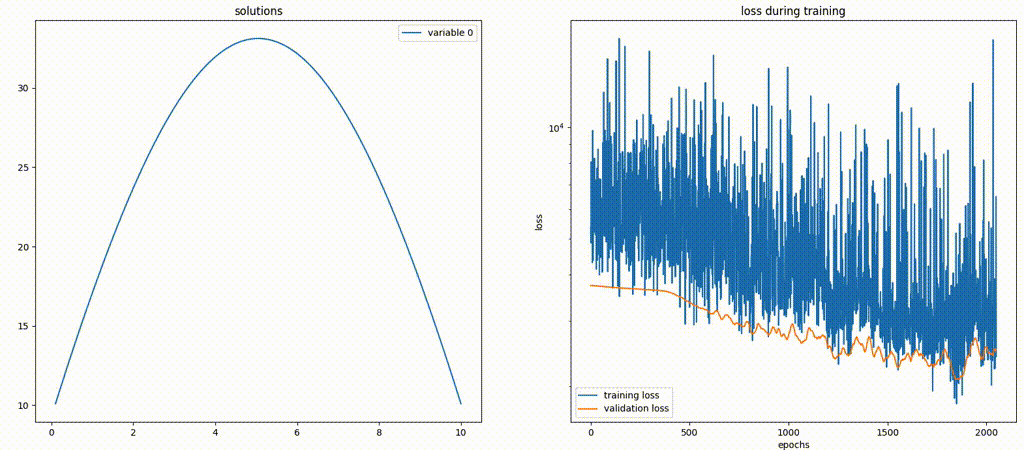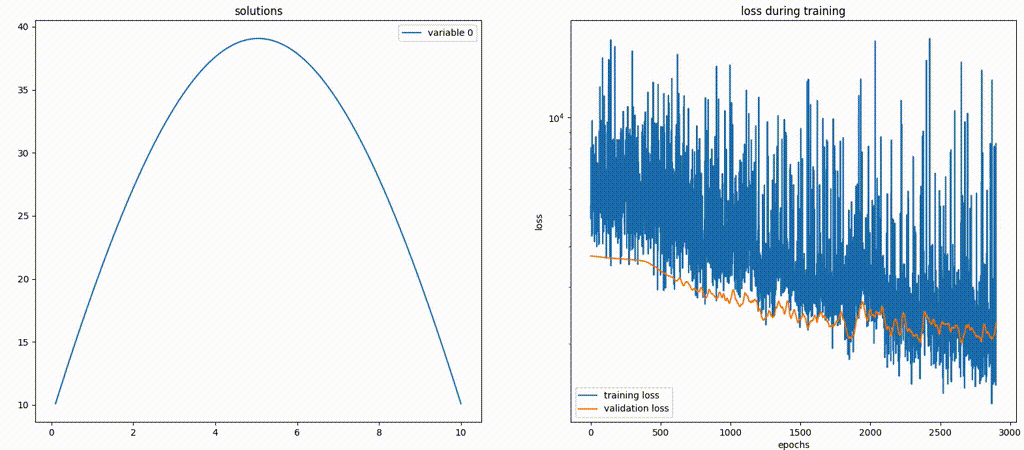
solver.fit(..., callbacks=[monitor.to_callback()])You should see the plots update every 100 epoch as well as on the last epoch, showing two plots — one for solution visualization on the interval [0,12] and the other for loss history (training and validation).
For convenience, we have implemented an FCNN – fully-connected neural network, whose hidden units and activation functions can be customized.
from neurodiffeq.networks import FCNN
# Default: n_input_units=1, n_output_units=1, hidden_units=[32, 32], activation=torch.nn.Tanh
net1 = FCNN(n_input_units=..., n_output_units=..., hidden_units=[..., ..., ...], activation=...)
...
nets = [net1, net2, ...]FCNN is usually a good starting point. For advanced users, solvers are compatible with any custom torch.nn.Module. The only constraints are:
-
The modules takes in a tensor of shape
(None, n_coords)and the outputs a tensor of shape(None, 1). -
There must be a total of
n_funcsmodules innetsto be passed tosolver = Solver(..., nets=nets).
Acutally, neurodiffeq has a single_net feature that doesn't obey the above rules, which won't be covered here.
Read the PyTorch tutorial on building your own network (a.k.a module) architecture.
Transfer learning is easily done by serializing old_solver.nets (a list of torch modules) to disk and then loading them and passing to a new solver:
old_solver.fit(max_epochs=...)
# ... dump `old_solver.nets` to disk
# ... load the networks from disk, store them in some `loaded_nets` variable
new_solver = Solver(..., nets=loaded_nets)
new_solver.fit(max_epochs=...)We currently working on wrapper functions to save/load networks and other internal variables of Solvers. In the meantime, you can read the PyTorch tutorial on saving and loading your networks.
In neurodiffeq, the networks are trained by minimizing loss (ODE/PDE residuals) evaluated on a set of points in the domain. The points are randonly resampled every time. To control the number, distribution, and bounding domain of sampled points, you can specify your own training/valiadation generators.
from neurodiffeq.generators import Generator1D
# Default t_min=0.0, t_max=1.0, method='uniform', noise_std=None
g1 = Generator1D(size=..., t_min=..., t_max=..., method=..., noise_std=...)
g2 = Generator1D(size=..., t_min=..., t_max=..., method=..., noise_std=...)
solver = Solver1D(..., train_generator=g1, valid_generator=g2)Here are some sample distributions of a Generator1D.
Generator1D(8192, 0.0, 1.0, method='uniform') |
Generator1D(8192, -1.0, 0.0, method='log-spaced-noisy', noise_std=1e-3) |
|---|---|
 |
 |
Note that when both train_generator and valid_generator are specified, t_min and t_max can be omitted in Solver1D(...). In fact, even if you pass t_min, t_max, train_generator, valid_generator together, the t_min and t_max will still be ignored.
Another nice feature of the generators is that you can concatenate them, for example
g1 = Generator2D((16, 16), xy_min=(0, 0), xy_max=(1, 1))
g2 = Generator2D((16, 16), xy_min=(1, 1), xy_max=(2, 2))
g = g1 + g2Here, g will be a generator that outputs the combined samples of g1 and g2
g1 |
g2 |
g1 + g2 |
|---|---|---|
 |
 |
 |
You can use Generator2D, Generator3D, etc. for sampling points in higher dimensions. But there's also another way
g1 = Generator1D(1024, 2.0, 3.0, method='uniform')
g2 = Generator1D(1024, 0.1, 1.0, method='log-spaced-noisy', noise_std=0.001)
g = g1 * g2Here, g will be a generator which yields 1024 points in a 2-D rectangle (2,3) × (0.1,1) every time. The x-coordinates of them are drawn from (2,3) using strategy uniform and the y-coordinate drawn from (0.1,1) using strategy log-spaced-noisy.
g1 |
g2 |
g1 * g2 |
|---|---|---|
 |
 |
 |
Sometimes, it is interesting to solve a bundle of equations at once. For example, you may want to solve differential equations of the form du/dt + λu = 0 under the initial condition u(0) = U0. You may want to solve this for all λ and U0 at once, by treating them as inputs to the neural networks.
One such application is for chemical reactions, where the reaction rate is unknown. Different reaction rates correspond to different solutions, and only one solution matches observed data points. You maybe interested in first solving for a bundle of solutions, and then determining the best reaction rates (aka equation parameters). The second step is known as the inverse problem.
Here's an example of how to do this using neurodiffeq:
-
Let's say we have an equation
du/dt + λu = 0and initial conditionu(0) = U0whereλandU0are unknown constants. We also have a set of observationst_obsandu_obs. We first importBundleSolverandBundleIVPwhich is necessary to obtaining a solution bundle:from neurodiffeq.conditions import BundleIVP from neurodiffeq.solvers import BundleSolver1D import matplotlib.pyplot as plt import numpy as np import torch from neurodiffeq import diff
-
We determine the domain of input
t, as well as the domain of parametersλandU0. We also need to make a decision of the order of the parameters. Namely, which should be the first parameter, and which should be the second. For the purpose of this demo, we chooseλto be the first parameter (index 0), andU0to be the second (index 1). It is very important to keep track of the indices of the parameters.T_MIN, T_MAX = 0, 1 LAMBDA_MIN, LAMBDA_MAX = 3, 5 # first parameter, index = 0 U0_MIN, U0_MAX = 0.2, 0.6 # second parameter, index = 1
-
We then define the
conditionsandsolveras usual, except that we useBundleIVPandBundleSolver1Dinstead ofIVPandSolver1D. The interface of these two is very similar toIVPandSolver1D. You can find out more in the API reference.# equation parameters comes after inputs (usually temporal and spatial coordinates) diff_eq = lambda u, t, lmd: [diff(u, t) + lmd * u] # The keyword argument must be named "u_0" in BundleIVP. If you use anything else, e.g. `y0`, `u0`, etc., it won't work. conditions = [ BundleIVP(t_0=0, u_0=None, bundle_param_lookup={'u_0': 1}) # u_0 has index 1 ] solver = BundleSolver1D( ode_system=diff_eq, conditions=conditions, t_min=T_MIN, t_max=T_MAX, theta_min=[LAMBDA_MIN, U0_MIN], # λ has index 0; u_0 has index 1 theta_max=[LAMBDA_MAX, U0_MAX], # λ has index 0; u_0 has index 1 eq_param_index=(0,), # λ is the only equation parameter, which has index 0 n_batches_valid=1, )
Since
λis a parameter in the equation andU0is a parameter in the initial condition, we must includeλin thediff_eqandU0in the condition. If a parameter is present in both the equation and the condition, it must be included in both places. All elements ofconditionspassed toBundleSovler1Dmust beBundle*conditions, even if they don't have parameters. -
Now, we can train it and obtain the solution as we normally would.
solver.fit(max_epochs=1000) solution = solver.get_solution(best=True)
The solution expects three inputs -
t,λandU0. All inputs must have the same shape. For example, if you are interested in fixingλ=4andU0=0.4and plotting the solutionuagainstt ∈ [0,1], you can do the followingt = np.linspace(0, 1) lmd = 4 * np.ones_like(t) u0 = 0.4 * np.ones_like(t) u = solution(t, lmd, u0, to_numpy=True) import matplotlib.pyplot as plt plt.plot(t, u)
-
Once you have a bundled
solution, you can find a set of parameters(λ, U0)that matches observed data points(t_i, u_i)most closely. This is achieved using simple gradient descent. In the following toy example, we assume there are only three data pointsu(0.2) = 0.273,u(0.5)=0.129, andu(0.8) = 0.0609. The following is classical PyTorch workflow.# observed data points t_obs = torch.tensor([0.2, 0.5, 0.8]).reshape(-1, 1) u_obs = torch.tensor([0.273, 0.129, 0.0609]).reshape(-1, 1) # random intialization of λ and U0; keep track of their gradient lmd_tensor = torch.rand(1) * (LAMBDA_MAX - LAMBDA_MIN) + LAMBDA_MIN u0_tensor = torch.rand(1) * (U0_MAX - U0_MIN) + U0_MIN adam = torch.optim.Adam([lmd_tensor.requires_grad_(True), u0_tensor.requires_grad_(True)], lr=1e-2) # run gradient descent for 10000 epochs for _ in range(10000): output = solution(t_obs, lmd_tensor * torch.ones_like(t_obs), u0_tensor * torch.ones_like(t_obs)) loss = ((output - u_obs) ** 2).mean() loss.backward() adam.step() adam.zero_grad() print(f"λ = {lmd_tensor.item()}, U0={u0_tensor.item()}, loss = {loss.item()}")
Simple. When importing neurodiffeq, the library automatically detects if CUDA is available on your machine. Since the library is based on PyTorch, it will set default tensor type to torch.cuda.DoubleTensor for if a compatible GPU device is found.
Refer to Sections Custom Networks and Transfer Learning.
The standard PyTorch way.
-
Build your networks as explained in Custom Networks:
nets = [FCNN(), FCN(), ...] -
Instantiate a custom optimizer and pass all parameters of these networks to it
parameters = [p for net in nets for p in net.parameters()] # list of paramters of all networks MY_LEARNING_RATE = 5e-3 optimizer = torch.optim.Adam(parameters, lr=MY_LEARNING_RATE, ...)
-
Pass BOTH your
netsand youroptimizerto the solver:solver = Solver1D(..., nets=nets, optimizer=optimizer)
Unlike traditional numerial methods (FEM, FVM, etc.), the NN-based solution requires some hypertuning. The library offers the utmost flexibility to try any combination of hyperparameters.
- To use a different network architecture, you can pass in your custom
torch.nn.Modules. - To use a different optimizer, you can pass in your own optimizer to
solver = Solver(..., optimizer=my_optim). - To use a different sampling distribution, you can use built-in generators or write your own generators from scratch.
- To use a different sampling size, you can tweak the generators or change
solver = Solver(..., n_batches_train). - To dynamically change hyperparameters during training, checkout our callbacks feature.
- Don't use
ReLUfor activation, because its second-order derivative is identically 0. - Re-scale your PDE/ODE in dimensionless form, preferably make everything range in
[0,1]. Working with a domain like[0,1000000]is prone to failure because a) PyTorch initializes the modules weights to be relatively small and b) most activation functions (like Sigmoid, Tanh, Swish) are most nonlinear near 0. - If your PDE/ODE is too complicated, consider trying curriculum learning. Start training your networks on a smaller domain, and then gradually expand until the whole domain is covered.
Everyone is welcome to contribute to this project.
When contributing to this repository, we consider the following process:
- Open an issue to discuss the change you are planning to make.
- Go through Contribution Guidelines.
- Make the change on a forked repository and update the README.md if changes are made to the interface.
- Open a pull request.