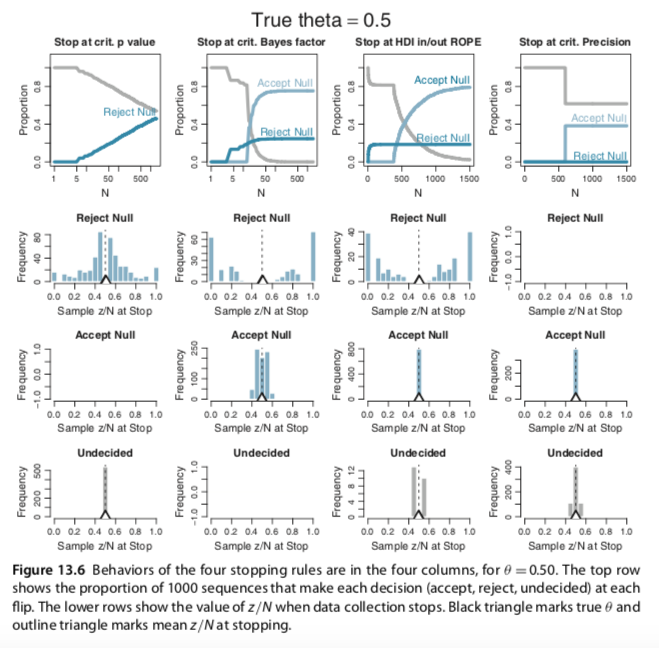
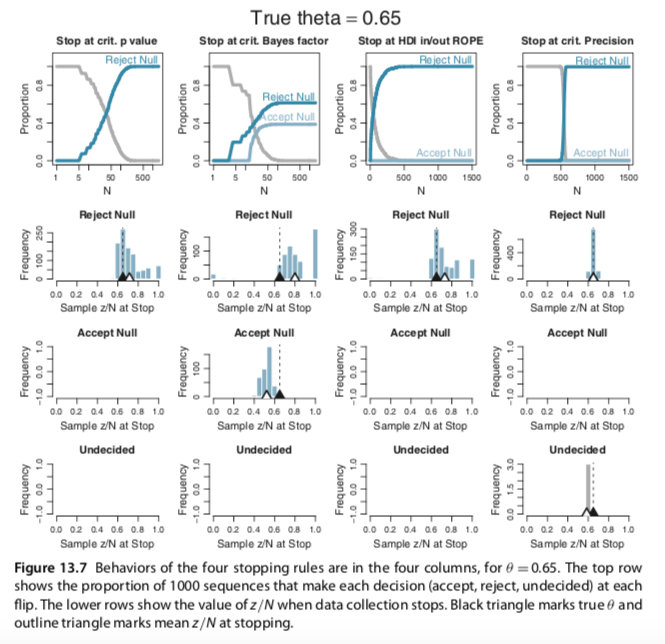
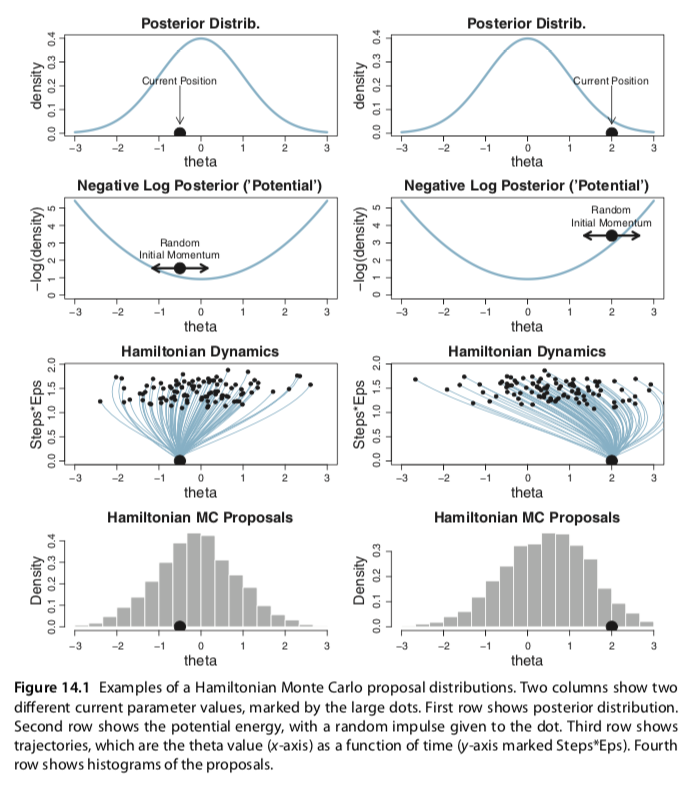
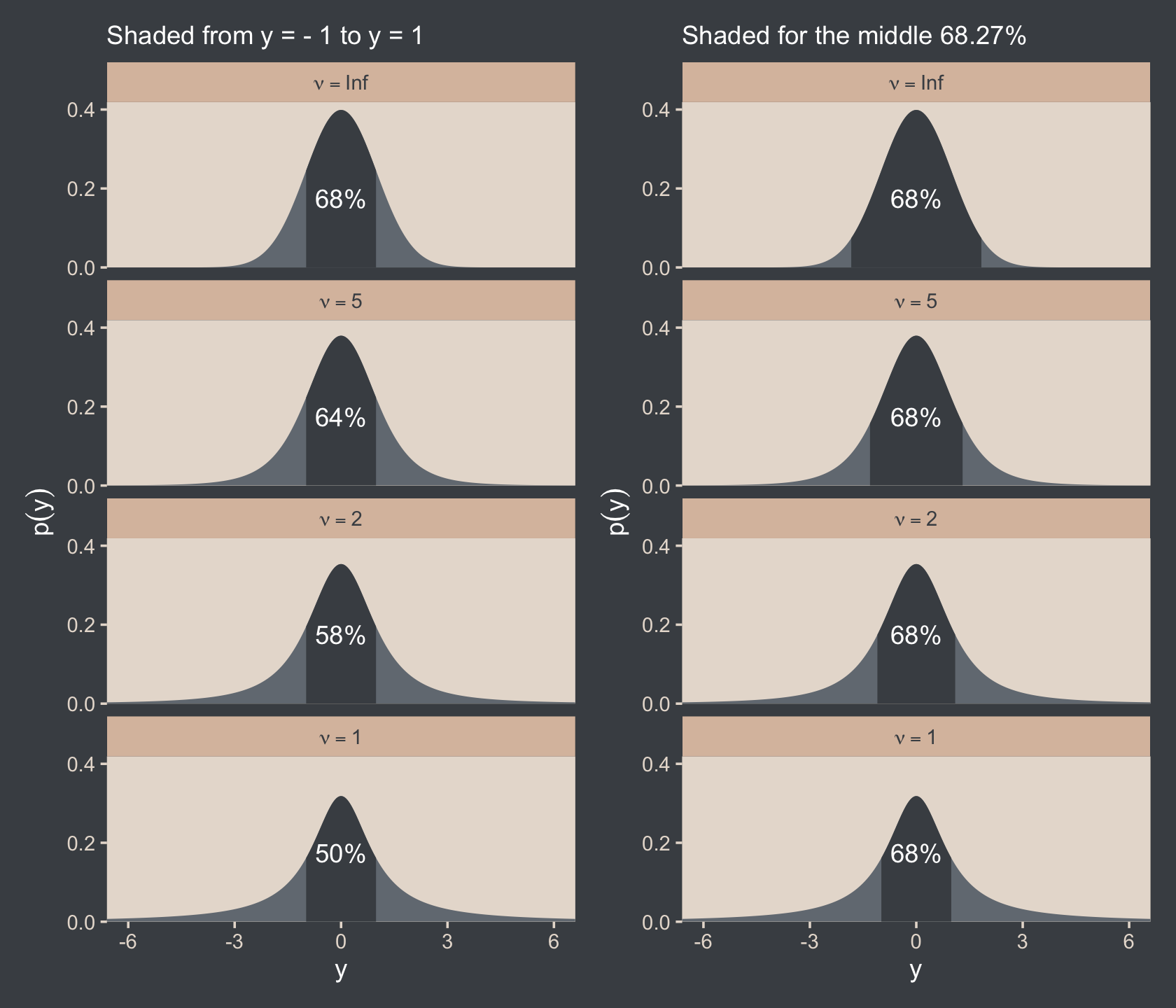
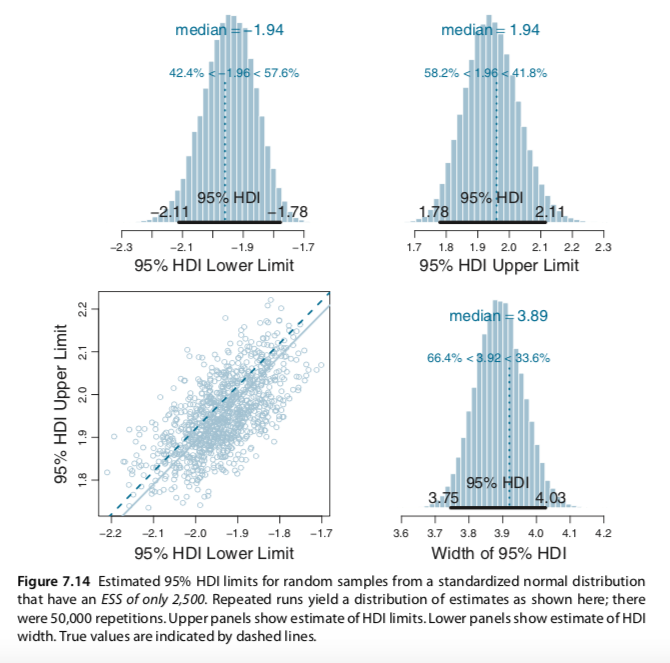
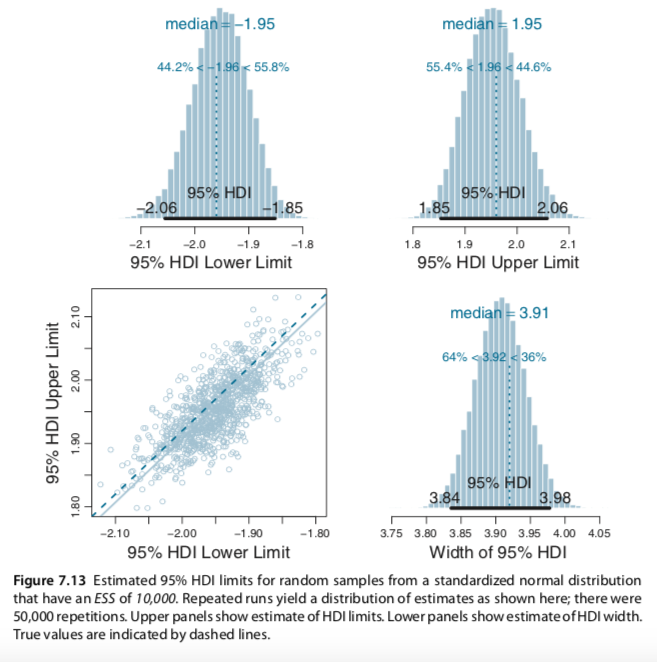
I slightly changed your codes for the Metropolis single-chain algorithm and reproduced several plots of figures 7.10 and 7.11 (page 179-180). In the bookdown, you have used brms to build the models and check for representativeness, so I am not sure if the Metropolis algorithm is useful to be added. Anyway, here it is:
library(tidyverse)
library(patchwork)
library(RColorBrewer)
library(coda)
# specify the data, to be used in the likelihood function.
my_data <- c(rep(0, 15), rep(1, 35))
# define the Bernoulli likelihood function, p(D|theta).
likelihood <- function(theta, data) {
z <- sum(data)
n <- length(data)
p_data_given_theta <- theta^z * (1 - theta)^(n - z)
p_data_given_theta[theta > 1 | theta < 0] <- 0
return(p_data_given_theta)
}
# define the prior density function.
prior_d <- function(theta) {
p_theta <- dbeta(theta, 1, 1)
p_theta[theta > 1 | theta < 0] = 0
return(p_theta)
}
# Define the relative probability of the target distribution. For our application,
# this target distribution is the unnormalized posterior distribution.
target_rel_prob <- function(theta, data) {
target_rel_prob <- likelihood(theta, data) * prior_d(theta)
return(target_rel_prob)
}
# specify the length of the trajectory, i.e., the number of jumps to try:
traj_length <- 50000
# initialize the vector that will store the results
trajectory1 <- rep(0, traj_length)
trajectory2 <- rep(0, traj_length)
trajectory3 <- rep(0, traj_length)
# specify where to start the trajectory:
trajectory1[1] <- 0.01 # another arbitrary value
trajectory2[1] <- 0.5 # another arbitrary value
trajectory3[1] <- 0.99 # another arbitrary value
# specify the burn-in period
burn_in <- ceiling(0.0 * traj_length) # arbitrary number, less than `traj_length`
# initialize accepted, rejected counters, just to monitor performance:
n_accepted1 <- 0
n_rejected1 <- 0
n_accepted2 <- 0
n_rejected2 <- 0
n_accepted3 <- 0
n_rejected3 <- 0
proposal_sd = .02
# now generate the random walk. the 't' index is time or trial in the walk.
#set.seed(47405)
for (t in 1:(traj_length - 1)) {
current_position1 <- trajectory1[t]
current_position2 <- trajectory2[t]
current_position3 <- trajectory3[t]
# use the proposal distribution to generate a proposed jump
proposed_jump1 <- rnorm(1, mean = 0, sd = proposal_sd)
proposed_jump2 <- rnorm(1, mean = 0, sd = proposal_sd)
proposed_jump3 <- rnorm(1, mean = 0, sd = proposal_sd)
# compute the probability of accepting the proposed jump
prob_accept1 <- min(1,
target_rel_prob(current_position1 + proposed_jump1, my_data)
/ target_rel_prob(current_position1, my_data))
prob_accept2 <- min(1,
target_rel_prob(current_position2 + proposed_jump2, my_data)
/ target_rel_prob(current_position2, my_data))
prob_accept3 <- min(1,
target_rel_prob(current_position3 + proposed_jump3, my_data)
/ target_rel_prob(current_position3, my_data))
# generate a random uniform value from the interval [0, 1] to
# decide whether or not to accept the proposed jump
# Chain 1......
if (runif(1) < prob_accept1) {
# accept the proposed jump
trajectory1[t + 1] <- current_position1 + proposed_jump1
# increment the accepted counter, just to monitor performance
if (t > burn_in) {n_accepted1 <- n_accepted1 + 1}
} else {
# reject the proposed jump, stay at current position
trajectory1[t + 1] <- current_position1
# increment the rejected counter, just to monitor performance
if (t > burn_in) {n_rejected1 <- n_rejected1 + 1}
}
# Chain 2........
if (runif(1) < prob_accept2) {
# accept the proposed jump
trajectory2[t + 1] <- current_position2 + proposed_jump2
# increment the accepted counter, just to monitor performance
if (t > burn_in) {n_accepted2 <- n_accepted2 + 1}
} else {
# reject the proposed jump, stay at current position
trajectory2[t + 1] <- current_position2
# increment the rejected counter, just to monitor performance
if (t > burn_in) {n_rejected2 <- n_rejected2 + 1}
}
# Chain 3........
if (runif(1) < prob_accept3) {
# accept the proposed jump
trajectory3[t + 1] <- current_position3 + proposed_jump3
# increment the accepted counter, just to monitor performance
if (t > burn_in) {n_accepted3 <- n_accepted3 + 1}
} else {
# reject the proposed jump, stay at current position
trajectory3[t + 1] <- current_position3
# increment the rejected counter, just to monitor performance
if (t > burn_in) {n_rejected3 <- n_rejected3 + 1}
}
# end of Metropolis algorithm
}
# extract the post-burn_in portion of the trajectory
accepted_traj1 <- trajectory1[(burn_in + 1) : length(trajectory1)]
accepted_traj2 <- trajectory2[(burn_in + 1) : length(trajectory2)]
accepted_traj3 <- trajectory3[(burn_in + 1) : length(trajectory3)]
# Convert all the chains into tibbles and then join all of them together
chain1 <- tibble(
chain = 1,
accepted_traj = accepted_traj1,
n_accepted = n_accepted1,
n_rejected = n_rejected1,
iter = rep(1:traj_length, times =1))
chain2 <- tibble(
chain = 2,
accepted_traj = accepted_traj2,
n_accepted = n_accepted2,
n_rejected = n_rejected2,
iter = rep(1:traj_length, times =1))
chain3 <- tibble(
chain = 3,
accepted_traj = accepted_traj3,
n_accepted = n_accepted3,
n_rejected = n_rejected3,
iter = rep(1:traj_length, times =1))
all_chains <- do.call("rbind", list(chain1, chain2, chain3)) %>%
mutate(chain= factor(chain))
# Calculate effectiveSize and MCSE: in the book ESS= 605.8 and MCSE = .00254
require(coda)
all_chains %>%
filter(iter %in% (500:10000)) %>%
summarise(eff_size = effectiveSize(accepted_traj),
mcse= sd(accepted_traj) / sqrt(eff_size))
# Now, let's do some plots
density_earlier_chain <- all_chains %>%
filter(iter < 500) %>%
ggplot(aes(x = accepted_traj)) +
geom_density(aes(color= chain)) +
tidybayes::stat_pointinterval(aes(y = 0, color= chain),
point_interval = mode_hdi, .width = .95) +
scale_x_continuous(breaks = seq(from = 0, to = 1, length.out = 6)) +
scale_y_continuous(NULL, breaks = NULL) +
labs(x = expression(theta), title= "Earlier Steps") +
theme(panel.grid = element_blank()) +
theme_classic()+
scale_color_brewer(palette = "PuBu")
density_later_chain <- all_chains %>%
filter(iter %in% (500:10000)) %>%
ggplot(aes(x = accepted_traj)) +
geom_density(aes(color= chain)) +
tidybayes::stat_pointinterval(aes(y = 0, color= chain),
point_interval = mode_hdi, .width = .95) +
scale_x_continuous(breaks = seq(from = 0, to = 1, length.out = 6)) +
scale_y_continuous(NULL, breaks = NULL) +
labs(x = expression(theta), title = "Later Steps") +
theme(panel.grid = element_blank()) +
theme_classic()+
scale_color_brewer(palette = "PuBu")
traceplot_earlier_chain <- all_chains %>%
ggplot(aes(x = accepted_traj, y = iter)) +
geom_path(size = 1/4, aes(color= chain)) + #color = "skyblue"
geom_point(size = .8, alpha = 1/2, aes(color= chain)) + #color = "skyblue"
coord_flip(xlim = c(0,1), ylim = c(1,500))+
scale_x_continuous(expression(theta), breaks = seq(from = 0, to = 1, length.out = 6)) +
labs(title = "Earlier Steps", y = "Iterations") +
theme(panel.grid = element_blank()) +
theme_classic() +
scale_color_brewer(palette = "PuBu")
traceplot_later_chain <- all_chains %>%
ggplot(aes(x = accepted_traj, y = iter)) +
geom_path(size = 1/4, aes(color= chain)) + #color = "skyblue"
geom_point(size = .8, alpha = 1/2, aes(color= chain)) + #color = "skyblue"
coord_flip(xlim = c(0,1), ylim = c(500,10000))+
scale_x_continuous(expression(theta), breaks = seq(from = 0, to = 1, length.out = 6)) +
labs(title = "Later Steps", y = "Iterations") +
theme(panel.grid = element_blank()) +
theme_classic() +
scale_color_brewer(palette = "PuBu")
(traceplot_earlier_chain + traceplot_later_chain)/(density_earlier_chain+density_later_chain) & theme(legend.position = "none")To draw a Gelman plot to check shrinkage factors, we can use the coda package. However, the graph is not as beautiful as the previous ones.